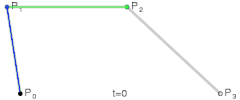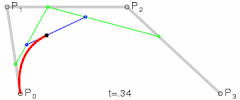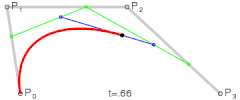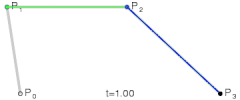
bezier curve
Bezier曲线很常用,一般2D绘图软件里都有。比如photoshop,flash之类。
它背后的原理简单的超乎想象,体现了数学的美妙。
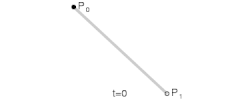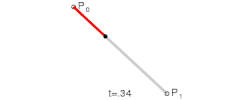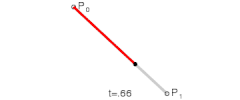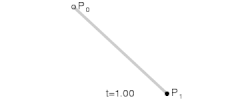
先从简单的开始,两个点之间进行线性插值。
[latex] B(t)=P_0+t(P_1-P_0)=(1-t)P_0+tP_1,tin[0,1] [/latex]
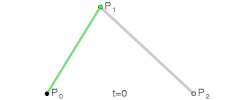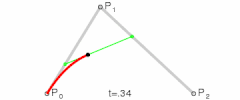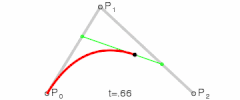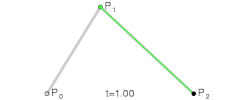
当然这是最简单的情形,如果扩展到三个点该如何插值呢?

从上面图片上可以看到,可以分成三步,从P0到P1进行上面的一维情形,得到点Q0,再从P1到P2,得到Q1,那么就有
[latex]Q_0=(1-t)P_0+tP_1[/latex]
[latex]Q_1=(1-t)P_1+tP_2[/latex]
然后再对Q0和Q1进行线性插值,得到点B
[latex]B=(1-t)Q_0+tQ_1=(1-t)^2P_0+2t(1-t)P_1+t^2P_2[/latex]
t从0到1增加,就得到了一条曲线,如下图
同样可以推广到四个点的情形,这样的曲线中,t的最高幂是三次。三次样条曲线用的最多,因为它提供了足够的可控制性和满足大部分场合的精度,同时又保持了相对的简单。
依照上面的方法,可以得到三次的情形
[latex]B(t)=(1-t)^3P_0+3(1-t)^2tP_1+3(1-t)t^2P_2+t^3P_3,tin[0,1][/latex]
这个时候可以注意到Pi点前面的系数,是不是似曾相识?没错,就是二项式公式。可以看成是相应次幂的[latex](1-t+t)^n[/latex]的展开。这个系数叫做Bernstein多项式。
最常用的三次曲线如下图,其中中间的两个就是控制点,在一些绘图软件里用钢笔拖出来的两条调整曲线形状的直线,就是调节中间两个点的位置。
[latex size=”2″]B(t)=sum_{i=0}^{n}{binom{n}{i}(1-t)^{n-i}t^iP_i}[/latex]
[latex size=”1″]=(1-t)^nP_0+binom{n}{1}(1-t)^{n-1}tP_1+..+t^nP_n,tin[0,1][/latex]
不过n大于3的时候就很少用了,除非在一些要求比较高的场合,比如飞机汽车线形的设计。
更多的资料,可以看这里
http://en.wikipedia.org/wiki/B%C3%A9zier_curve